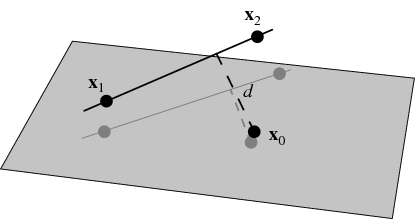
equation is (Equation 13.1 in the book):

q' = q + (d - q.n)n

where q is the point to test to the line
q' is the closest point on the line
d is the distance ?? but not known how to calculate
n is the normal of the line

the issue is that d is not explained, if I had d then I could easily project it from q with (n * -1) to get the point on the line... but it doesn't explain d.

in chapter 13.3 "Closest point on Plane" it says that "We learned how to compute the distance from a point to a plane in Section 12.5.4" but when I checked out 12.5.4 it gives me the equation (12.14):

a = q.n - d

but again, doesn't explain what d is...

any help would be good thanks, I'm sure I'm just missing something. I've read through the sections but I couldn't find anything, except for...

"If we assume n is a unit vector, then the distance from p to q (and thus, the distance from q to the plane) is simply a."

but to get a, I need d?? this is weird... lol

------------------
"But it is God who judges: He brings one down, he exalts another." - Psalm 75:7

Crazy -- I've read your post a couple of times, and I'm having a bit of trouble understanding it (though I'm not sure any worse than you are).

It sounds like you've got a line in 3d space, and you have another point that is your target, and so you're trying to solve for the nearest point to the target that is a point on the original line.

If that's the case, you may find the Mathworld explanation helpful:


Point-Line Distance (3-Dimensional)

I've learned a fair bit of math from that site -- particularly having to do with things like fractals and soddy circles. Really great stuff, I highly recommend it.

Does that help at all? Or am I completely off base?

--clint

Edit: Oh yeah -- BTW, here's their formula for d:

Not sure if it's the same d, but it's a start. Explanation of that formula is on the above page that I linked.

[This message has been edited by HanClinto (edited July 31, 2006).]

though with that line, it is illustrated via two points. which would be fine I guess, except I'm wanting to do it via a point (point on the line) and then a normal, and for 2d if that helps make it any easier...

so a line would look something like this:

vector2d point; // vector2d would just be a float x, y;
vector2d normal;

and then the point would just be a vector2d.

you could think of it as like a 2d plane of sorts... sort of like a ray, but bi-directional. I was considering just doing 2 ray checks, but it would be a lot better if I could just figure out what that 'd' from "3D Math Primer..." was on about.

Would you happen to have an equation for closest point to 3d plane?? where the plane is illustrated as similar to the line (above) but with vector3d (float x, y, z) for the point and normal. I'm checking out that site atm, thanks for the link.

When you going on your trip? Hope you have a great time.

------------------
"But it is God who judges: He brings one down, he exalts another." - Psalm 75:7

Point-Plane Distance

Though there is also:

Point-Line Distance 2D

Leaving for Ghana tomorrow evening -- pretty exciting schtuff.

--clint

Thanks for you help clint, but I just backtracked through the book (3D Math Primer) to section 12.2.3 to discover d is the "signed distance from the origin to the line"...

Thanks again though for your help.

Have a great holiday!!!

------------------
"But it is God who judges: He brings one down, he exalts another." - Psalm 75:7